Fast LISA Response Tutorial
[1]:
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
import h5py
from fastlisaresponse import pyResponseTDI, ResponseWrapper
from astropy import units as un
from lisatools.detector import EqualArmlengthOrbits, ESAOrbits
YRSID_SI = 31558149.763545603
This tutorial provides information on using fastlisaresponse: a generic time-domain LISA response function, including both projection on to constellation arms and TDI combinations. It is also GPU/CPU agnostic. The GPU capability is helpful for use in Bayesian inference algorithms. For more information and a detailed API, please see the documentation.
If you use this code, please cite arXiv:2204.06633 and the code’s Zenodo.
Warning: newest version (1.0.9) of code with lisatools orbits needs detailed testing before deployed for a paper.
Gravitational wave signal
fastlisaresponse takes any time domain signal in the form \(h(t) = h_+ + ih_\times\). We are going to use a Galactic binary waveform given by
where \(A\) is the amplitude; \(\iota\) is the inclination; and
\(f\) is the initial gravitational wave frequency, and the over-dots are its time derivatives. The initial phase is \(\phi_0\).
This waveform is then transformed to the solar-system barycenter (SSB) frame with the polarization angle, \(\psi\):
The waveform here is called with a class to allow for GPU usage. Equivalently, you can just use a function. However, please note that the function must take the keyword arguments T and dt which are the total observation time in in years and the sampling rate in seconds (inverse of the sampling frequency).
[2]:
class GBWave:
def __init__(self, use_gpu=False):
if use_gpu:
self.xp = xp
else:
self.xp = np
def __call__(self, A, f, fdot, iota, phi0, psi, T=1.0, dt=10.0):
# get the t array
t = self.xp.arange(0.0, T * YRSID_SI, dt)
cos2psi = self.xp.cos(2.0 * psi)
sin2psi = self.xp.sin(2.0 * psi)
cosiota = self.xp.cos(iota)
fddot = 11.0 / 3.0 * fdot ** 2 / f
# phi0 is phi(t = 0) not phi(t = t0)
phase = (
2 * np.pi * (f * t + 1.0 / 2.0 * fdot * t ** 2 + 1.0 / 6.0 * fddot * t ** 3)
- phi0
)
hSp = -self.xp.cos(phase) * A * (1.0 + cosiota * cosiota)
hSc = -self.xp.sin(phase) * 2.0 * A * cosiota
hp = hSp * cos2psi - hSc * sin2psi
hc = hSp * sin2psi + hSc * cos2psi
return hp + 1j * hc
[3]:
gb = GBWave(use_gpu=False)
Build waveforms
We will now move on to the response. The method and specific maths used to determine the response function can be found in our paper: arXiv:2204.06633. We recommend accessing the response through the fastlisaresponse.ResponseWrapper. You can access the response function itself through fastlisaresponse.pyTDIResponse. See the documentation for using this class directly as it is a bit more complicated. If you only need to use the projection portion or the TDI part, then you should access the response class itself. Otherwise, the wrapper should be fine. You can access the projections from the wrapper if need.
Setup classes
First we will setup everything to properly compute the response function for Galactic binary waveforms.
[14]:
use_gpu = False
T = 2.0 # years
t0 = 10000.0 # time at which signal starts (chops off data at start of waveform where information is not correct)
sampling_frequency = 0.1
dt = 1 / sampling_frequency
# order of the langrangian interpolation
order = 25
# 1st or 2nd or custom (see docs for custom)
tdi_gen = "2nd generation"
index_lambda = 6
index_beta = 7
tdi_kwargs_esa = dict(
order=order, tdi=tdi_gen, tdi_chan="AET",
)
gb_lisa_esa = ResponseWrapper(
gb,
T,
dt,
index_lambda,
index_beta,
t0=t0,
flip_hx=False, # set to True if waveform is h+ - ihx
use_gpu=use_gpu,
remove_sky_coords=True, # True if the waveform generator does not take sky coordinates
is_ecliptic_latitude=True, # False if using polar angle (theta)
remove_garbage=True, # removes the beginning of the signal that has bad information
orbits=EqualArmlengthOrbits(),
**tdi_kwargs_esa,
)
# define GB parameters
A = 1.084702251e-22
f = 2.35962078e-3
fdot = 1.47197271e-17
iota = 1.11820901
phi0 = 4.91128699
psi = 2.3290324
beta = 0.9805742971871619
lam = 5.22979888
Run generator
[15]:
chans = gb_lisa_esa(A, f, fdot, iota, phi0, psi, lam, beta)
Plot results
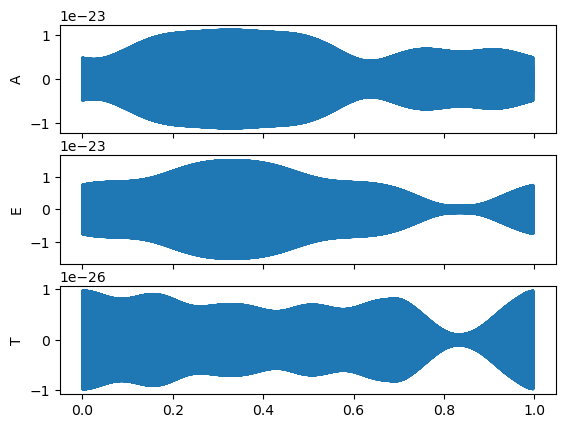
[16]:
%matplotlib inline
fig, ax = plt.subplots(3, 1, sharex=True)
for i, lab in enumerate(["A", "E", "T"]):
ax[i].plot(np.arange(len(chans[0])) * dt / YRSID_SI, chans[i])
ax[i].set_ylabel(lab)
Custom TDI setup
Here is an example of the 2nd Generation TDI implementation within the code.
[7]:
X1 = [
{"link": 13, "links_for_delay": [], "sign": +1},
{"link": 31, "links_for_delay": [13], "sign": +1},
{"link": 12, "links_for_delay": [13, 31], "sign": +1},
{"link": 21, "links_for_delay": [13, 31, 12], "sign": +1},
{"link": 12, "links_for_delay": [], "sign": -1},
{"link": 21, "links_for_delay": [12], "sign": -1},
{"link": 13, "links_for_delay": [12, 21], "sign": -1},
{"link": 31, "links_for_delay": [12, 21, 13], "sign": -1},
]
X2 = X1 + [
{"link": 12, "links_for_delay": [13, 31, 12, 21], "sign": +1},
{"link": 21, "links_for_delay": [13, 31, 12, 21, 12], "sign": +1},
{
"link": 13,
"links_for_delay": [13, 31, 12, 21, 12, 21],
"sign": +1,
},
{
"link": 31,
"links_for_delay": [13, 31, 12, 21, 12, 21, 13],
"sign": +1,
},
{"link": 13, "links_for_delay": [12, 21, 13, 31], "sign": -1},
{"link": 13, "links_for_delay": [12, 21, 13, 31, 13], "sign": -1},
{
"link": 13,
"links_for_delay": [12, 21, 13, 31, 13, 31],
"sign": -1,
},
{
"link": 13,
"links_for_delay": [12, 21, 13, 31, 13, 31, 12],
"sign": -1,
},
]
tdi_kwargs_custom = dict(
order=order, tdi=X2, tdi_chan="AET",
)
gb_lisa_custom = ResponseWrapper(
gb,
T,
t0,
dt,
index_lambda,
index_beta,
flip_hx=False, # set to True if waveform is h+ - ihx
use_gpu=use_gpu,
remove_sky_coords=True, # True if the waveform generator does not take sky coordinates
is_ecliptic_latitude=True, # False if using polar angle (theta)
remove_garbage=True, # removes the beginning of the signal that has bad information
orbits=EqualArmlengthOrbits(),
**tdi_kwargs_custom,
)
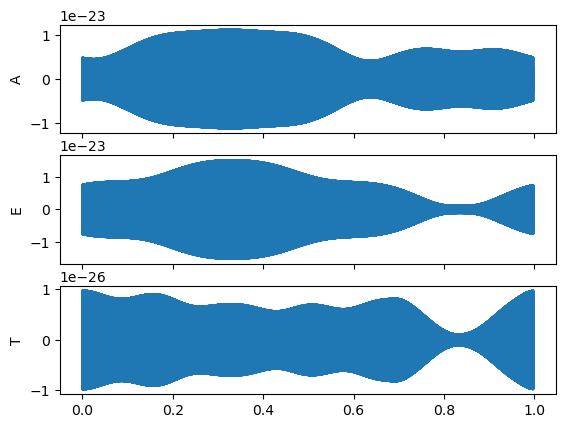
chans = gb_lisa_esa(A, f, fdot, iota, phi0, psi, lam, beta)
fig, ax = plt.subplots(3, 1, sharex=True)
for i, lab in enumerate(["A", "E", "T"]):
ax[i].plot(np.arange(len(chans[0])) * dt / YRSID_SI, chans[i])
ax[i].set_ylabel(lab)